Linear  Algebra  III

In this problem we will perform basic matrix calculus.

We begin by stating a few rules we will use. Everywhere the notation $x_i$ refers to the $i^{\rm th}$ component of a vector ${\mathbf x}$ and $x_{i,j}$ refers to the $(i,j)^{\rm th}$ component of a matrix ${\mathbf X}$.

1. The derivative of a scalar $z$ with respect to an $N \times 1$ vector ${\mathbf x}$ is an $N \times 1$ vector. The $i^{\rm th}$ component of this vector is $\frac{dz}{dx_i}$.
2. The derivative of a scalar $z$ with respect to an $N \times M$ matrix ${\mathbf X}$ is an $N \times M$ matrix, whose $(i,j)^{\rm th}$ component is $\frac{dz}{dx_{i,j}}$.
3. The derivative of an $N \times 1$ vector ${\mathbf y}$ with respect to an $M \times 1$ vector ${\mathbf x}$ is an $N \times M$ matrix, whose $(i,j)^{\rm th}$ component is $\frac{dy_i}{dx_j}$.

Note the order of the indices in the following

4. The derivative of an $N \times 1$ vector ${\mathbf y}$ with respect to an $M \times L$ matrix ${\mathbf X}$ is an $N \times L \times M$ tensor (note the reversal of the order of $L$ and $M$), whose $(i,j,k)^{\rm th}$ component is $\frac{dy_i}{dx_{k,j}}$ (again, note the reversal of the order of indices in the denominator -- to get the derivative in the $i,j,k$ location, we differentiate w.r.t to the variable in the $k,j$ location of ${\mathbf X}$.
5. The derivative of an $N \times K$ matrix ${\mathbf Y}$ with respect to an $M \times L$ matrix ${\mathbf Y}$ is an $N \times K \times L \times M$ tensor, whose $(i,j,k,l)^{\rm th}$ component is $\frac{dy_{i,j}}{dx_{l,k}}$.
6. The derivative of an $N_1 \times N_2 \times \cdots \times N_L$ tensor ${\mathbf Y}$ with respect to an $M_1\times M_2 \times \cdots \times M_K$ tensor is an $N_1 \times N_2 \times \cdots \times N_L \times M_K \times M_{K-1} \times \cdots \times M_1$ tensor.

The transpose of any $N_1 \times N_2$ matrix is an $N_2 \times N_1$ matrix. We will represent the transposition operation by the superscript $\top$. Let ${\mathbf Y} = {\mathbf X}^\top$. Then $y_{i,j} = x_{j,i}$ ({\em i.e.} the $(i,j)$-th component of ${\mathbf Y}$ is the $(j,i)$-th component of ${\mathbf X}$.

For the purposes of the computation here, we will expand the notion of transposes to tensors. Let ${\mathbf Y}$ be any $N_1 \times N_2 \times \cdots \times N_K$ tensor. By our definition ${\mathbf X} = {\mathbf Y}^\top$ is an $N_K \times N_{K-1} \times \cdots \times N_1$ tensor, whose components are given by $x_{i_1,i_2,\cdots,i_K} = y_{i_K,i_{K-1},\cdots,i_i}$.

Using the above definitions, we can also write the following chain rule.

7. Let ${\mathbf X}$ be any matrix (noting that a vector is also a one-column matrix, so the same rule also applies to vectors, or tensors in general). Let $g(\bullet)$ and $h(\bullet)$ be two functions. The functions may have scalar, vector or tensor outputs. Let \[ y = g\left(h\left( {\mathbf X}\right)\right) \] Then \[ \frac{dy}{d{\mathbf X}} = \left(\frac{dh({\mathbf X})}{d{\mathbf X}}\right) ^{\top} \frac{d g}{dh} \] where $dg$ is shorthand for $d(g(h({\mathbf X})))$ and $dh$ stands for $d(h({\mathbf X}))$. Note the order of multplication.
8. In general, if $f_1(\bullet)$, $f_2(\bullet)$, $f_3(\bullet) \cdots$ are functions, then if \[ y = f_1\left(f_2\left(f_3\left(\cdots f_K\left({\mathbf X}\right)\right)\right)\right) \] then \[ \frac{dy}{d{\mathbf X}} = \left(\frac{df_K({\mathbf X})}{d{\mathbf X}}\right)^\top \left( \frac{d f_{K-1}}{df_K}\right)^\top \left(\frac{d f_{K-2}}{df_{K-1}}\right)^\top \cdots \left(\frac{d f_2}{d f_1}\right)^\top \frac{d f_1}{df_2} \] Once again, note the order of computation.

Finally, we give the following rule for multiplying tensors.

9. Let ${\mathbf X}$ be an $N \times M \times L$ tensor. It can only left multiply $L \times 1$ vectors. Let ${\mathbf y}$ be an $L \times 1$ vector. Then ${\mathbf Z} = {\mathbf Xy}$ is an $N\times M$ matrix whose components are given by \[ z_{i,j} = \sum_k x_{i,j,k}y_k \]
10. Let ${\mathbf X}$ be an $N \times M \times L$ tensor. It can only left multiply $L \times M$ matrices. Let ${\mathbf Y}$ be an $L \times M$ matrix. Then ${\mathbf Z} = {\mathbf XY}$ is an $N\times 1$ vector whose components are given by \[ z_i = \sum_j\sum_k x_{i,j,k}y_{k,j} \]

We are now set to state our problems.

A.   Derivative of scalar function w.r.t. vector argument

Let ${\mathbf x}$ and ${\mathbf y}$ be $N\times 1$ vectors. Let \[ e = \| z - {\mathbf y}^\top{\mathbf x}\|^2 \] Show that \[ \frac{de}{d{\mathbf x}} = -2\left(z - {\mathbf y}^\top{\mathbf x}\right) {\mathbf y} \] The derivation is simple, based on rule number 1.

B.   Derivative of scalar function w.r.t. matrix argument

Let ${\mathbf X}$ be an $N\times M$ matrix, ${\mathbf z}$ be an $N \times 1$ vector, ${\mathbf y}$ be $M\times 1$ vectors. Let \[ e = \| {\mathbf z} - {\mathbf X}{\mathbf y}\|^2 \] Show that \[ \frac{de}{d{\mathbf X}} = -2\left({\mathbf z} - {\mathbf X}{\mathbf y}\right) {\mathbf y}^\top \]

HINT:

For part B., the chain rule gives us: \[ \frac{de}{d{\mathbf X}} = \left(\frac{d{\mathbf X}{\mathbf y}}{d{\mathbf X}}\right)^\top \frac {d \| {\mathbf z} - {\mathbf X}{\mathbf y}\|^2} {d{\mathbf X}{\mathbf y}} \] Note that ${\mathbf X}{\mathbf y}$ is an $N \times 1$ vector whose $i^{\rm th}$ component is given by $\sum_j x_{i,j}y_j$. Therefore, representing ${\mathbf u} = {\mathbf X}{\mathbf y}$, \[ \frac {d u_i}{d x_{j,k}} = \begin{cases} y_k~~~~if~~j=i\\ 0~~~~~otherwise \end{cases} \] Thus, although $\frac{d{\mathbf u}}{\mathbf X}$ is an $N \times M \times N$ tensor, only the entries along the diagonal plane $i=j$ are non-zero, and all other terms are zero. That is, if we let ${\mathbf V} = \frac{d{\mathbf u}}{{\mathbf X}}$, using rule 4 we get \[ v_{i,k,j} = \begin{cases} y_k~~~~if~~i=j\\ 0~~~~~otherwise \end{cases} \] The resulting Tensor has the structure shown below. Only the diagonal plane shown in the figure has non-zero values. All the remaining values are 0. Each row in the diagonal plane is the vector ${\mathbf y}^\top$.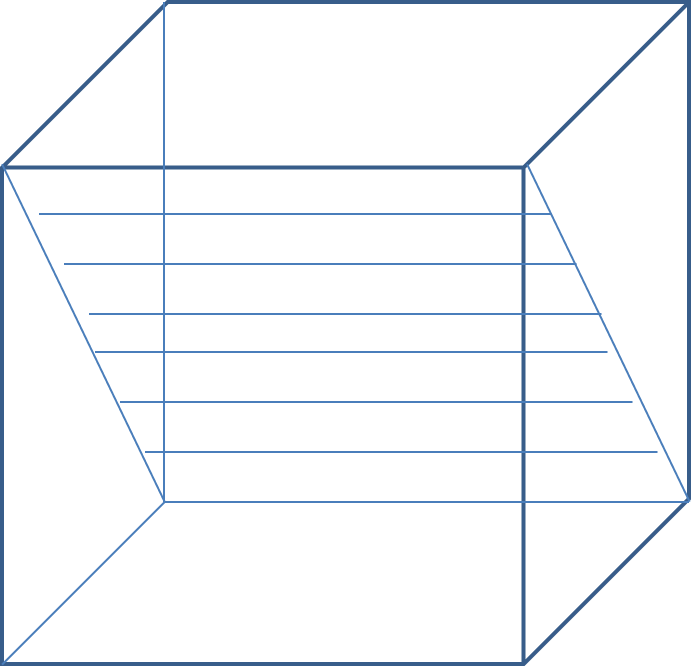

Because of the zero-valued off diagonal elements, tensor transposition has no effect on the tensor. Multiplying this tensor with any $M\times 1$ vector ${\mathbf t}$ has the following geometric interpretation. The figure below illustrates the operations.

The depth dimension of the tensor, which is its trailing dimension, multiplies the vector. The highlighted points and the arrows indicate corresponding elements that are multiplied together. The products are summed.

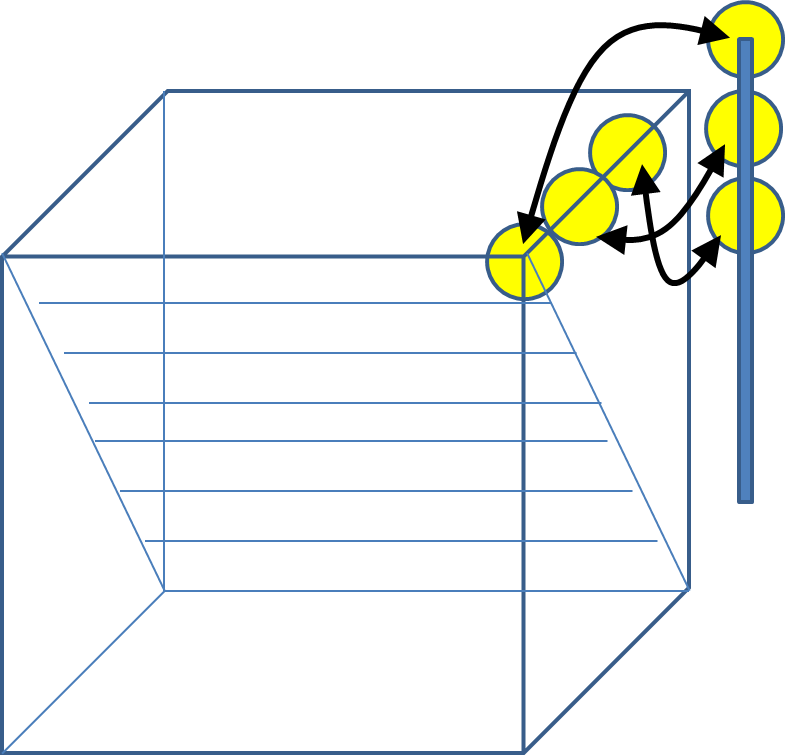
Clearly, since only the diagonal elements have non-zero values, only one of the component-wise products has a non-zero value, and the sum takes this value.

This has the effect that for any $M \times 1$ vector ${\mathbf t}$, the matrix ${\mathbf S} = {\mathbf V}^\top{\mathbf t}$ is an $M \times N$ matrix whose components (according to rule 9) are given by \[ s_{k,j} = \sum_{i} v_{i,j,k}t_i = t_ky_j \] The indices can be verified by referring to the illustration above.